Infrarot Entfernungsmesser

Die Firma Sharp bietet mit der GP2D.. Reihe einige einfach anzusteuernde Infrarotentfernungsmesser an. Dabei wird zu Bestimmung der Entfernung nicht gemessen wie viel Licht von dem Objekt reflektiert wird, sondern in welchem Winkel es reflektiert wird. Dies hat den Vorteil, dass der Sensor relativ unabhängig von der Oberfläche ist (im Gegensatz zu dem IS471F).

Ich habe mal alle Typen in einer kleinen Tabelle gegenübergestellt:

Typ	Ausgang	Messbereich	Schaltabstand
GP2D12	Analog	10-80cm	-
GP2Y0A21YK	Analog	10-80cm	-
GP2D02	Digital 8-bit	10-80cm	-
GP2D05	Digital 1-bit	10-80cm	kann mittels Poti verstellt werden
GP2D120	Analog	4-30cm	-
GP2D150	Digital 1-bit	3-30cm	15cm
GP2Y0A02YK	Analog	20-150cm	-
GP2Y0D02YK	Digital 1-bit	20-150cm	80cm

Für alle diese Typen gilt:
Betriebsspannung: 4.5 bis 7.0 Volt
Abmessungen: 45mm x 14mm x16mm

Funktionsprinzip

Alle Sensoren funktionieren nach demselben Prinzip: Der Emitter sendet einen Infrarotstrahl aus. Trifft der Lichtstrahl auf kein Objekt, wird er auch nicht reflektiert, der Empfänger zeigt also auch kein Objekt an. Wird das Licht jedoch an einem Objekt reflektiert, kehrt es zum Empfänger zurück und es entsteht ein Dreieck zwischen dem Reflektionspunkt, dem Emitter und dem Empfänger. Das ganze kann man sich folgendermaßen vorstellen:

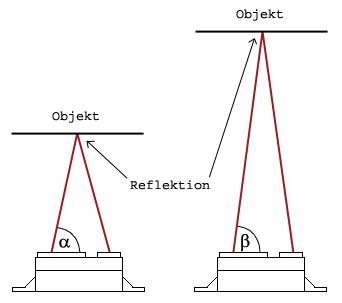
Mit Hilfe des Winkels zwischen dem Auftreffenden Strahl und dem Sensor lässt sich jetzt die Entfernung des Objektes von dem Sensor bestimmen:

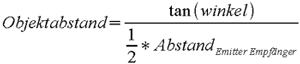
$Objektabstand = 2 * tan(winkel) / Abstand_{Sender zu Empfänger}$

Formel

Ich habe mal zu einem GP2D120 (Messbereich 4 bis 30 cm, analoger Ausgang) bei V_CC und A_REF = 5,1 Volt Messwerte zu den verschiedenen Entfernungen ermittelt:

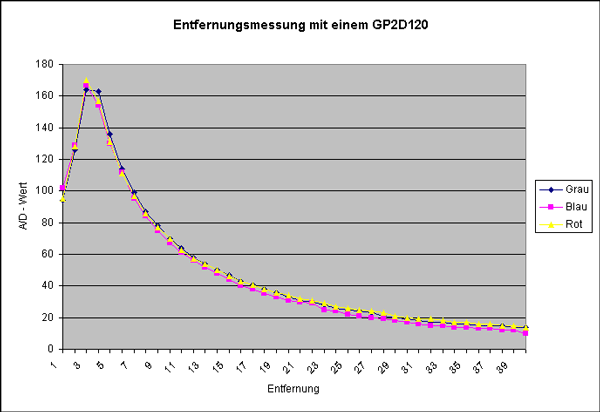
Wie man sieht ist die Ausgangsspannung des Sensor nicht proportional zur Entfernung. Außerdem kann man erkennen, dass die Wert bei einer Entfernung kleiner als ungefähr 4 cm stark abfallen, sodass man diesem Bereich nicht mehr zur Entfernungsmessung benutzen kann.

Was auch auffällt ist, dass die Wert nicht von den Reflektionseigenschaften des Hindernisses abhängen. Ich habe auch ausprobiert das Hindernis zu drehen. Selbst dabei sind die Messwerte realtiv konstant geblieben.

Wenn man aber die Entfernung braucht muss man den Wert den der Analog/Digital Wandler des Mikroprozessors liefert umrechnen. Dies kann man mit einer recht einfachen Näherungsformel tun:

Formel

D = A/(X-B)

D ist die Entfernung
X ist der Ausgabewert des Sensors
A ist die Steigung der Kurve A/X
B ist der Offset der Kurve

Ermitteln der Konstanten A und B:

A = (X'-X) D'D/(D-D')
B = (D'X' - DX)/(D' - D)

D und X sind die Entfernung und der Ausgabewert der ersten Messung (z.B. Bei 8 cm)
D' und X' sind die Entfernung und der Ausgabewert der zweiten Messung (z.B. bei 30 cm)

Bei meinem Sensor ergaben sich damit folgende Werte für A und B:

A = 730,9
B = -5,4

Die damit erreichte Genauigkeit kann sich sehen lassen:

Berechnete Werte

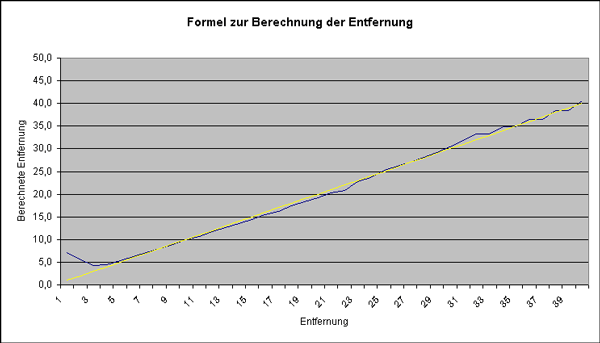
Gelb ist die korrekte Kurve. Blau ist die aus den Messwerten errechnete Entfernung. Auch hier kann man erkennen, dass der Fehler in dem Bereich unter 4 cm zu groß ist.

Der durchschnittliche Fehler liegt damit bei mir bei ca. 0,7 cm. Der maximale Fehler im Bereich über 4 cm liegt bei 1,2 cm, allerdings wird der Fehler im Bereich über 35 cm immer größer. Dies hängt damit zusammen, dass dort die Messwerte sehr dicht bei einander liegen (siehe oberes Diagramm).

Zum Anfang

Kommentare

# Christian Dreyer meinte am 5. Februar 2007, 16:05 dazu:

Super Info sehr hilfsreich.

# Andre meinte am 23. März 2008, 22:57 dazu:

Einfach aber Präzise. Danke für die Info!

# krakos meinte am 22. April 2008, 22:30 dazu:

Danke für die Erklärung!
Was mir noch unklar ist, Licht breitet sich doch wellenförmig aus. Der GP2Y0D02YK hat ja z.B. einen Messbereich von 130cm, ohne Laser kann man das Licht doch nicht so genau in dem Bereich auf einen Punkt fokussieren, oder? Wie funktioniert das genau?

# hans meinte am 20. Mai 2008, 20:17 dazu:

hi, diese art der umrechnung klingt ja richtig gut. habe auf anderen seiten einen ansatz mittels linearer regression gefunden. etwas umständlicher als dieses verfahren. weiß jemand ob beide verfahren einen gemeinsamen zusammenhang haben oder inwiefern sie sich im ergebnis unterscheiden?

# Fabian Greif meinte am 26. Mai 2008, 13:01 dazu:

Ich habe gerade mal nach linearer Regression gesucht:
Lineare Regression bzw. die Regressionsanalyse ganz allgemein ermöglicht es aus Eingangswerten und einem Modell für den Zusammenhang zwischen Messwerten und Ausgabewert die “besten” Parameter für das Modell zu finden. Im linearen Fall ist das Modell eine einfache Gerade.

Die Lineare Regression müsste daher soweit ich das verstanden habe aber für dieses Problem ungeeignet sein, da die Messwerte keine Gerade beschreiben. Da nützen auch die besten Parameter für diese Gerade nichts. Die Funktion gleich viel eher einer Hyperbel, daher der oben beschriebene Ansatz.

Hast du mal einen Link zu einer der erwähnten Seite wo lineare Regression verwendet wird?

# Norbert meinte am 28. Mai 2008, 15:24 dazu:

In Excel kannst man sich unter dem Menupunk ?Diagramme? zu den Messwerten eine Trendlinie anzeigen lassen die anhand z.B. linearer, logarithmischer u.a. Regression gebildet wird. Weiterhin läßt sich auch die dazugehörige Funktionsgleichung ausgeben.

kreatives-chaos.com

Themen:

Infrarot Entfernungsmesser

Funktionsprinzip

Formel

Berechnete Werte

Kommentare

Deine Meinung:

Lizenz